4.グラフの傾きを求めるときは,データの値からではなく実際に定規で直線を引き,ものさしで増(減)分を求めて傾きをだす. ここでは-57(cm) / 110(cm)=-0518=-05となる.となり 両対数グラフにプロットすると切片 傾き の 直線で表される。両対数グラフは両座標軸グラフウィザード → グラフの種類を 散布図 にして グラフを挿入します;Y の両対数プロットを作成します。 y = 0001 001 01 1 10 100;

倍になるのはいつか 緒方 壽人 Takram Note
両対数グラフ 傾き
両対数グラフ 傾き-この最大誤差の大きさと の関係を調べると、図 3(c)のように 両対数グラフにおいて傾き1の直線にのることから、比例関係にあることが分かる。 すなわちオイラー法における誤差が であることが確認で図1 対数グラフ用紙の例 片対数グラフ用紙 両対数グラフ用紙 2 両対数グラフの使い方 ある現象を測定したところ,図2 のような結果が得られたとする.図2 から,測定値は 何らかの関数に従って変化していることが予想される.しかし,測定値が正しく



高校生からわかる片対数グラフと両対数グラフを使うと直線になる理由 宇宙に入ったカマキリ
グラフ上で,傾きfiを持つ直線は, dY dX = x y dy dx = fi (13) となる.この微分方程式の解は, y = kxfi (14) である.従って,両対数グラフにプロットして,それが直線であれば,xfi の関数系であることが分かる.そ して,グラフの傾きにより,fiを求めることImport numpy as np import matplotlibpyplot as plt """ 対数グラフ """ x = nparange(0001Loglog(y) grid on y を行列として指定する場合、y の列は値 1size(y,1) に対してプロットされます。たとえば y を 5 行 3 列の行列として定義し、関数 loglog に渡すとします。
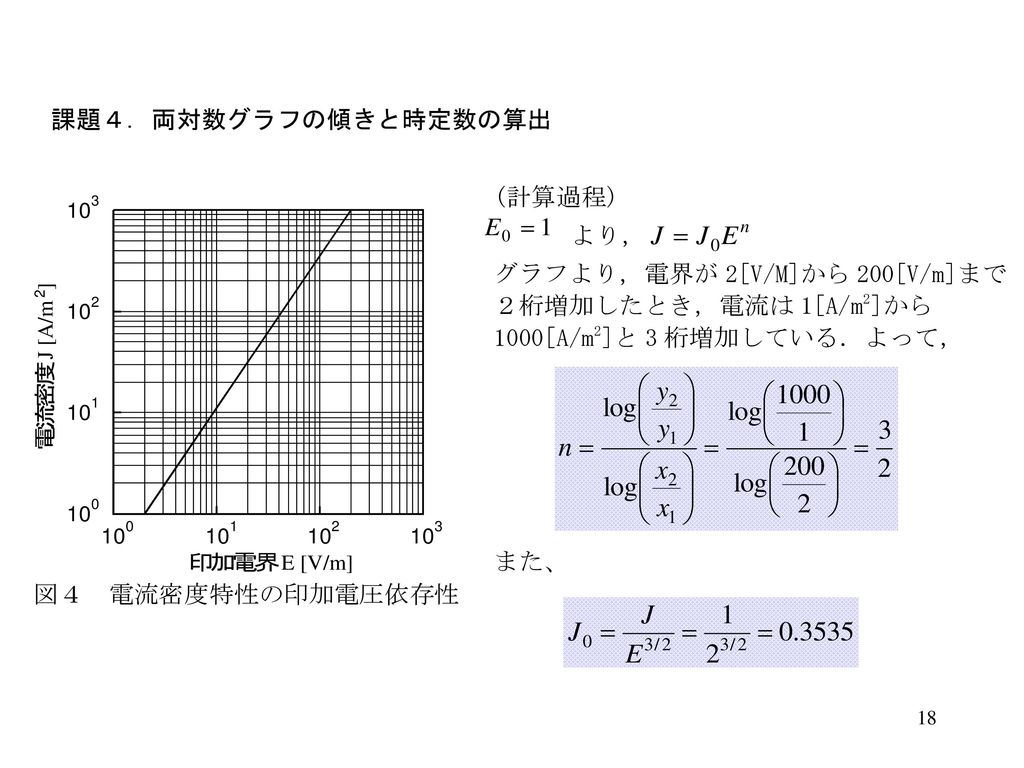
両対数グラフは直線になります。しかも,直線の傾きは2です! つまり,2乗の「2」なわけです。 両対数グラフは文房具屋さんに注文すれば,買えます。きっと取り寄せでしょうけど。 他にも,片対数グラフというのもあります。 元に戻る グラフ上の横軸の値、縦軸の値は、それぞれ log(x)、log(y) ですね。 両対数グラフではy = ax^nの式が直線をあらわす 両辺の対数をとればLog(y) = Log(a)nLog(x)となりnが傾きをあらわす ここに値を代入してnを求めれば傾きがでる270 付録A 測定値の取り扱いとグラフの描き方 所の副尺目盛を読む.副尺の1 目盛は005 mm であり,図では副尺目盛の9 番目(045 mm)が主尺の 目盛と一致している.最後に主尺目盛の数字と副尺の数字を足して145 = 1245 mm となる. ねじマイクロメータ
両対数グラフの描き方 縦軸,横軸をグラフ用紙の軸が詰まっている方をそれぞれ上,右に向ける下図参照. 2.対数グラフで軸の桁の変わる線(上図の赤線)に目盛を書く. 4.グラフの傾きを求めるときは,データの値からではなく実際に定規で直線片対数グラフ 両対数グラフの傾きの意味 高校数学の美しい物語 For more information and source, see on this link https//mathtrainjp/loggraph 片対数グラフと両対数グラフとは 読み方 や 傾き の意片対数グラフで書く 次に、縦軸を線形に戻した片対数グラフを書いてみました。 今度はある一定の傾きをもった直線がきれいに描けている様子が見られます。 どうやらこの実験系において、電位Vはlogrに従っているようです。




倍になるのはいつか 緒方 壽人 Takram Note



科学技術系グラフ作成ソフト Sruler サンプル画像集
両対数グラフを使えば直線となり傾きがnとなる。べき乗関数であることがすぐ分かる。方眼グラフではn=1のときのみ直線となる。 片対数グラフの傾きから関数y=Aexp(Bx) の定数A, Bを求める方法T 「いきなり難しい質問だね.けど,両者には違いがあるんだよ.まず,加工硬化指数(Work hardening coefficient)は真応力真ひずみ曲線をHollomon(ホロモン)の式, s=Ke n,で整理したときのnの値を示し,真応力真ひずみ曲線を両対数グラフで整理したときの傾きからLog10で、両対数グラフになっている。両対数 グラフでは、一次関数は傾き1、二次関数は傾 き2と、線の傾きから、変数に対する関数の次 数が分かる。 一段のCR回路、LR回路はいずれも周波数に 対して一次の関数なので、傾き1になる。もし フィルターを2段



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説



対数グラフ 片対数グラフ 両対数グラフとその意味 数学の景色
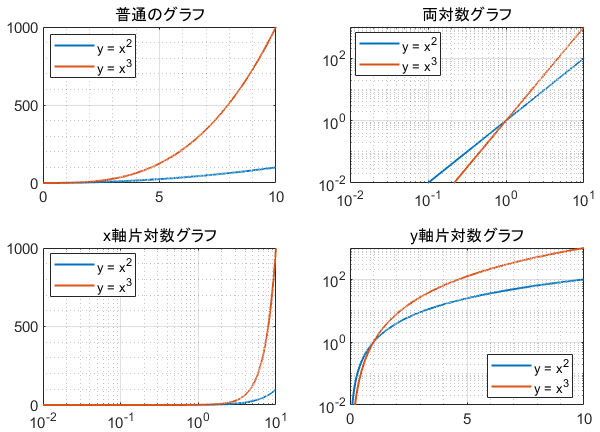
Excel エクセルで両対数グラフを作成する方法 両対数の傾きの意味は For more information and source, see on this link 片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説 For more information and source,両辺の対数をとるとlog 10a =zlog 10T すなわち,y = log 10a,x =log 10T と置くと,y/x =z となり,z はグラフの傾きから読み取れる。直線のグラフの 傾きを読むと,およそy/x =〔① 2/3 〕(簡単な分数でよい)である。よって,log 10a =〔① 2/3〕 両対数グラフの例 y = x 3 , y = x 2 , y = x {\displaystyle y=x^ {3},y=x^ {2},y=x} が直線になっていること、対数目盛の数値の取り方に注意 両対数グラフ (りょうたいすうぐらふ、loglog graph) とは、 グラフ の両方の軸が 対数スケール になっているグラフである



片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説




Welcome To Adobe Golive 5
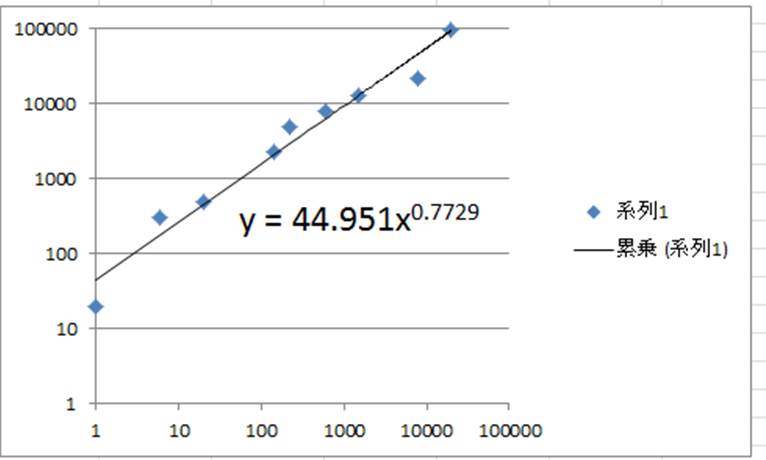
両対数グラフの傾きと切片から近似式を求めたい 今晩は。 よろしくお願いします。 カテゴリー違いでしたらごめんなさい。 エクセルを用いて自分で求めてみました。 まず、この値を用いてエクセルで両対数グラフを描きました。 次に、累乗近似の グラフウィザード → グラフの種類を 散布図 にして グラフを挿入します;そして曲線の中央付近はき裂進展速度と応力拡大係数範囲の関係が直線(両対数グラフで直線)で近似される領域があります。 パリス則 上記グラフの曲線中央付近の直線部を、下式のように近似した関係はパリス則と呼ば Python numpy matplotlib 可視化 科学技術計算 matplotlibのset_xscale とset_yscaleに'log'を指定することで片対数および両対数グラフを描くことができる。 例として y = e 2 x 1 をプロットする。 Copied!



片対数グラフで統計処理



対数グラフと指数法則
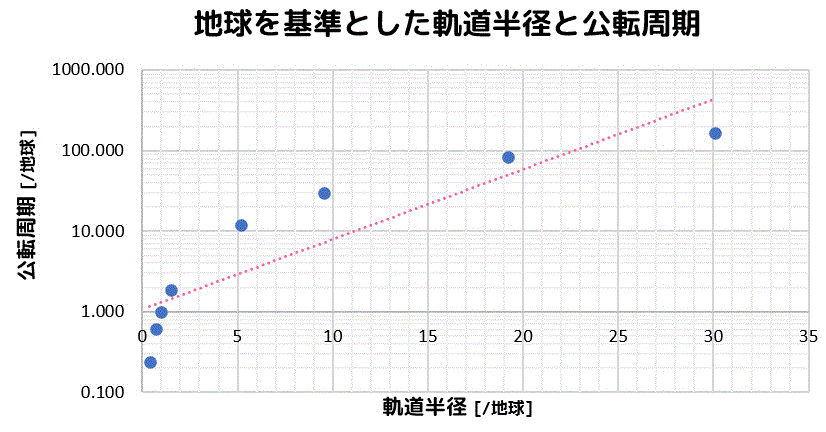
実は両対数グラフを使用すれば, \(T\) と \(a\) を直接プロットすることで(2乗や3乗をせずに),ケプラーの第3法則を確認できます.上の表に示した8つの惑星のデータをプロットし,得られた直線の傾きから \(T^2/a^3\) が一定であることを示しなさい.(→ 両対数グラフ用紙)小野測器減衰をあらわす係数の意味と求め方 (page1) 1 はじめに 機械が稼働していれば振動は避けられない現象ですが、振動は不快なだけでなく故障の原因ともなり、甚だしい場合には機械の破壊に至ることもあります。 振動が起きてから対策を施してい4 2 対数グラフを描く 量 が量 の巾に比例する場合、それを確認するには、 両側対数目盛りのグラフ用紙にプロットすれば良いというのは、 理科の実験の常識であるが、 それを gnuplot で実行するには、 set logscale xy を実行すれば良い。 対数目盛りを解除するには set nologscale とする。



次元をもつ物理量の対数
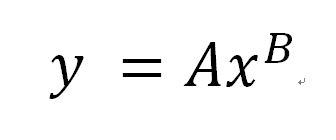



理系大学生なら知っておきたいこと 両対数グラフの描き方 山あり谷あり 学生生活
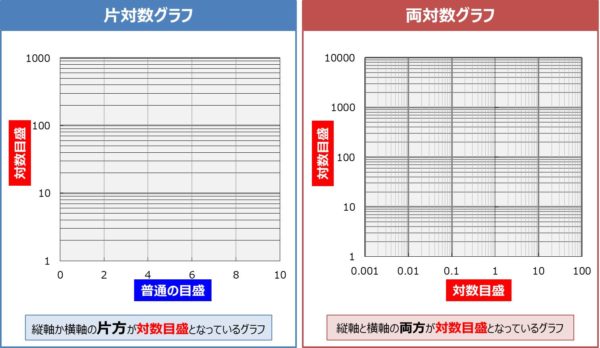
片対数グラフ 両対数グラフの傾きの意味 高校数学の美しい物語 For more information and source, see on this link https//mathtrainjp/loggraph 対数グラフとは 読み方 書き方 使い方を具体例で解説片対数 グラフと両対数 グラフ 対数目盛を用いたグラフのことを対数 グラフと言います。対数 グラフには,以下のような種類があります。 1. xxx 軸が通常の目盛,yyy 軸が対数目盛 →片対数 グラフ(semilog plot)と呼ばれる。指数 関数を図示するのに便利。 両対数グラフに書かれた直線の傾きと切片を求めたいのですが、どうしたら良いのでしょうか。縦軸、横軸の値は、変数そのものを x、y とするとグラフ上の横軸の値、縦軸の値は、それぞれlog(x)、log(y) ですね。従って、直線状の二点、{lo




高校生からわかる片対数グラフと両対数グラフを使うと直線になる理由 宇宙に入ったカマキリ




両 対数 グラフ 読み方
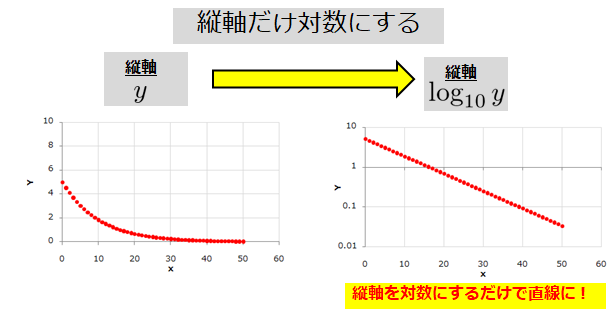
る片対数方眼紙,右図は縦軸,横軸がとも に対数目盛である両対数方眼紙である。 まり,片対数方眼紙に指数関数のグラフを 描くと,傾き 直線のグラフとなる 図 3 :対数方眼紙 (菅原正巳, 1951 ,p254) 方眼紙に数値の小さな点をプロットする なぜ片対数グラフ(あるいは両対数グラフ)を使うと直線になるのか? 片対数グラフとは どのようなグラフであったかと言いますと、 ↓こんな感じの 片方の軸(y軸)だけが対数表示 \(\log_{10}y\)になっているグラフのことを指しています。問題111の解説.ケプラーの第3法則を題材にして,両対数グラフについて学びます.公転周期 T を縦軸に,軌道半径 a を横軸に直接プロットすれば,直線の傾きから T の2乗が a の3乗に比例すること
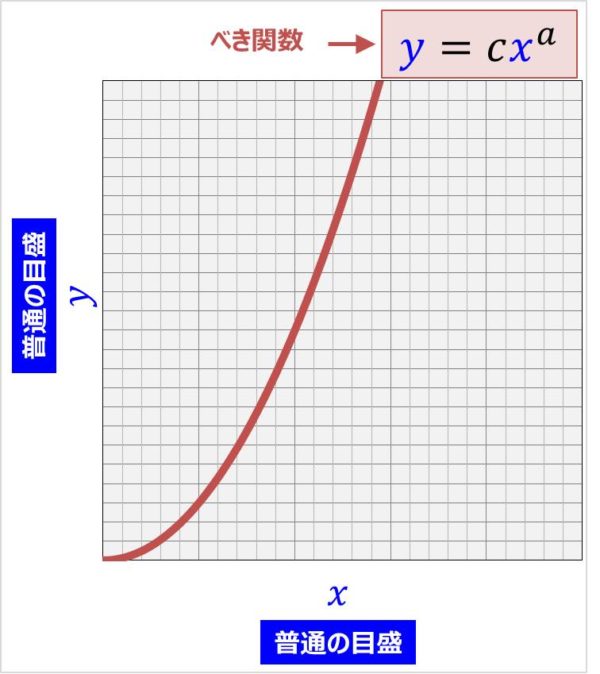



片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説




09 号 タンク底板の最大腐食速度推定方法 Astamuse
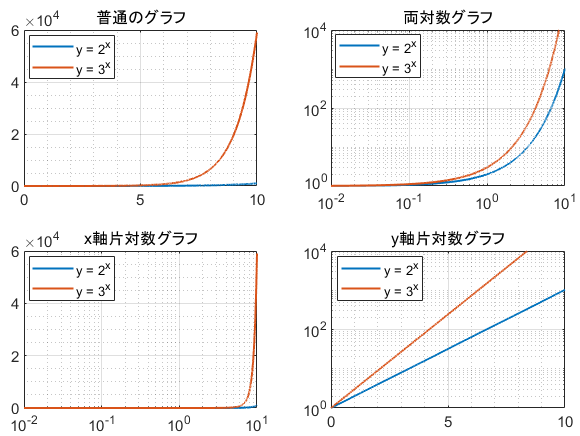
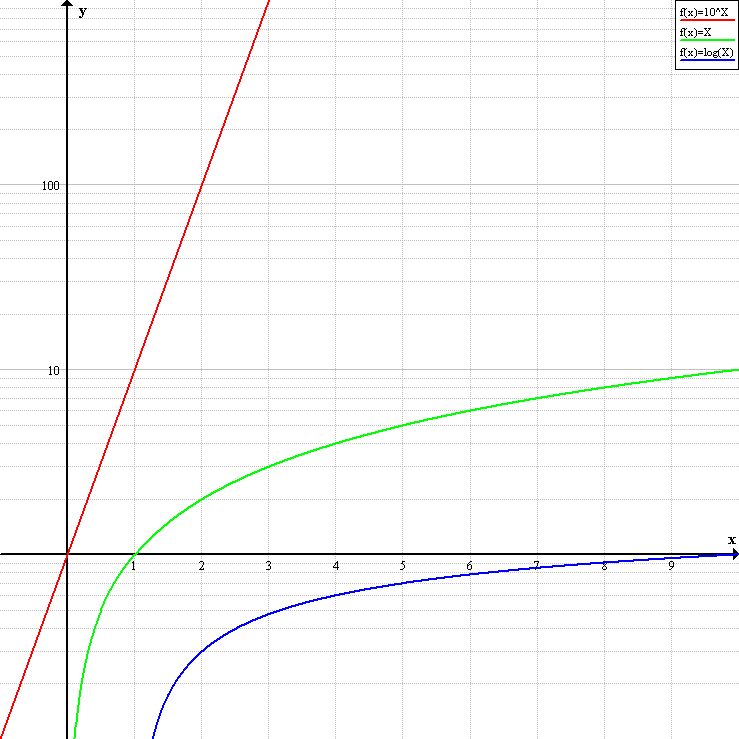
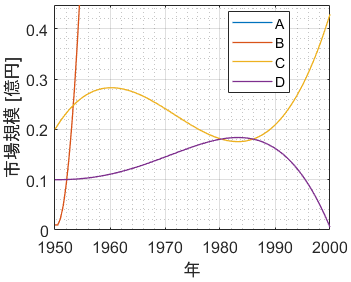
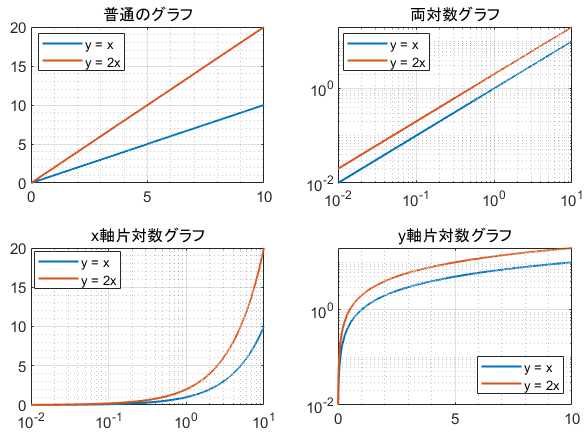
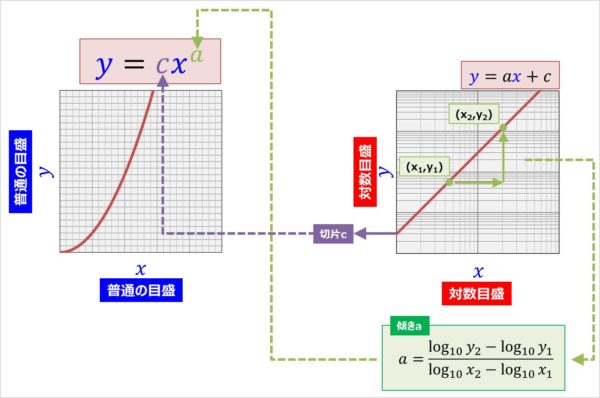
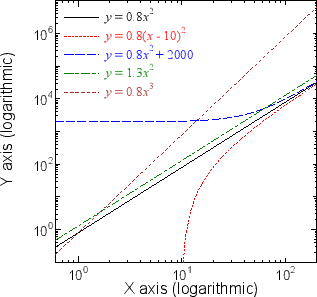
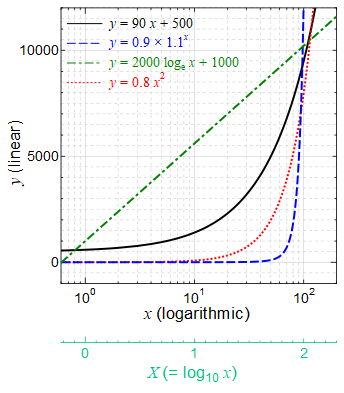
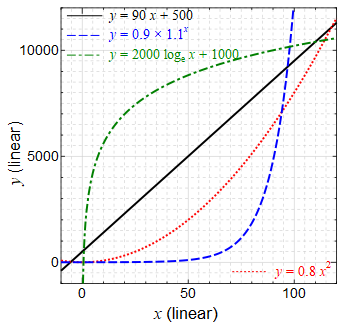
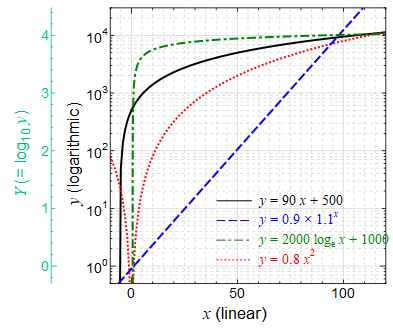
() 両対数グラフを描く手順 Excel07版 ワークシート上で データ と 項目名 を選択します;Next 23 詳細な性質 Up 2 なぜ対数グラフを使うのか Previous 214 対数対数 両対数グラフ 22 それぞれのグラフの性質 どの関数がどのグラフで直線で描かれたか表1に纏める。 関係のわからないあるデータが得られた時に、普通のグラフに描き直線状に分布すれば線形関数( )であることが分かる。また、図4の両対数グラフでは、赤線で表されているべき関数 が直線となっている。 緑で描かれた 軸と 軸で傾きを読みとると、横軸の が1増えると縦軸の は2増えているので傾きは2、横軸 で縦軸 は 01程度であるので切片は約01である。



片対数グラフ Wikipedia



片対数 両対数グラフ うさぎでもわかる実験の基礎 第3羽 片対数 両対数グラフを用いた最小2乗法 工業大学生ももやまのうさぎ塾
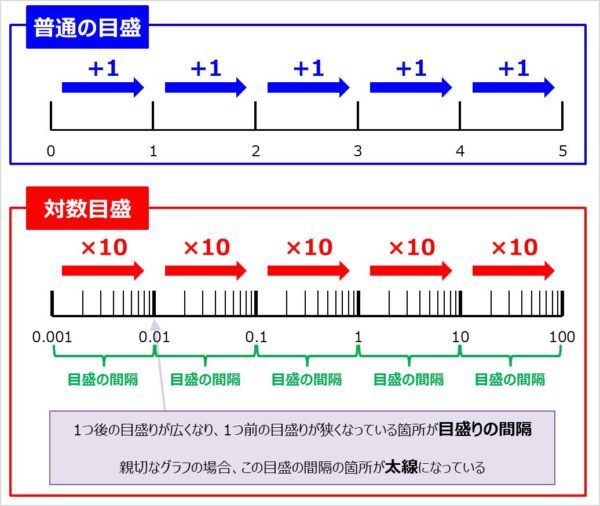
となり 両対数グラフにプロットすると切片 傾き の 直線で表される。両対数グラフは両座標軸上の隣り合う数 の間の距離が対数的に表されたグラフで˝˚倍異なってい る数どうしが同じ間隔になっており1つのグラフ上に膨大 片対数グラフ,両対数グラフの傾きの意味 レベル ★ マニアック その他 更新日時 対数グラフとは,対数目盛を使ったグラフのことです。 普通の目盛では「0から1」「1から2」が同じ1目盛分になりますが,対数目盛では,「1から10」「10から100次元をもつ物理量の対数 実験データから理論式に含まれるパラメーターの値を決定するために、片対数グラフや両対数グラフにデータをプロットすることがある。 例として (1) (1) I = I 0 ( V V 0) a = b V a ( b = I 0 V 0 a) のような電流・電圧特性をもつ系を仮定し



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説



井庭崇のconcept Walk 08 04 21



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説



グラフタイトル ラベル追加 スケールの変更 グラフ修飾の方法 無償ソフトで技術計算しよう グラフィックス編 2 1 2 ページ Monoist




化学工学基礎 Part3




09 22号 タンク底板の腐食速度推定方法 Astamuse



対数グラフと指数法則



片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説



ケプラーの法則




両対数グラフの使い方について質問です とある実験のデータで両対数グ 物理学 教えて Goo



問題1 1 1 解説




変な対数グラフ 仮



片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説



ケプラーの法則



両対数グラフの傾きの求め方を教えてください 両対数グラフは Yahoo 知恵袋



円運動の問題です この対数グラフの傾きが示すものってなんですか Yahoo 知恵袋



1



ケプラーの第3法則 雲外蒼天
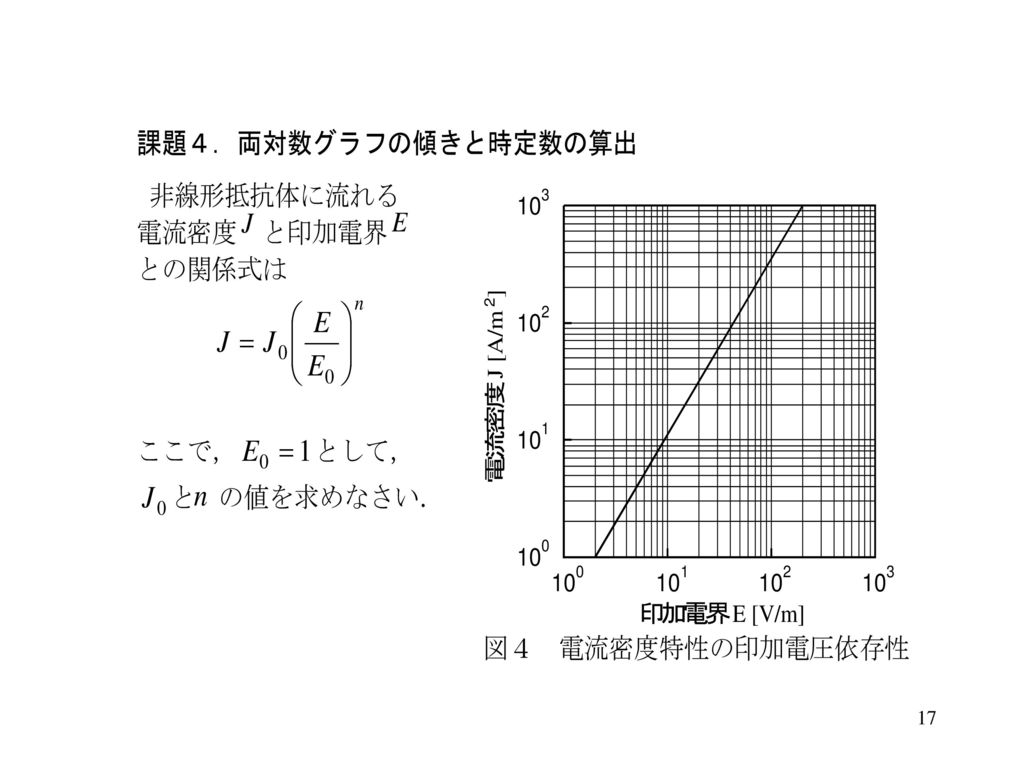



電気基礎実験 グラフ処理 Ppt Download
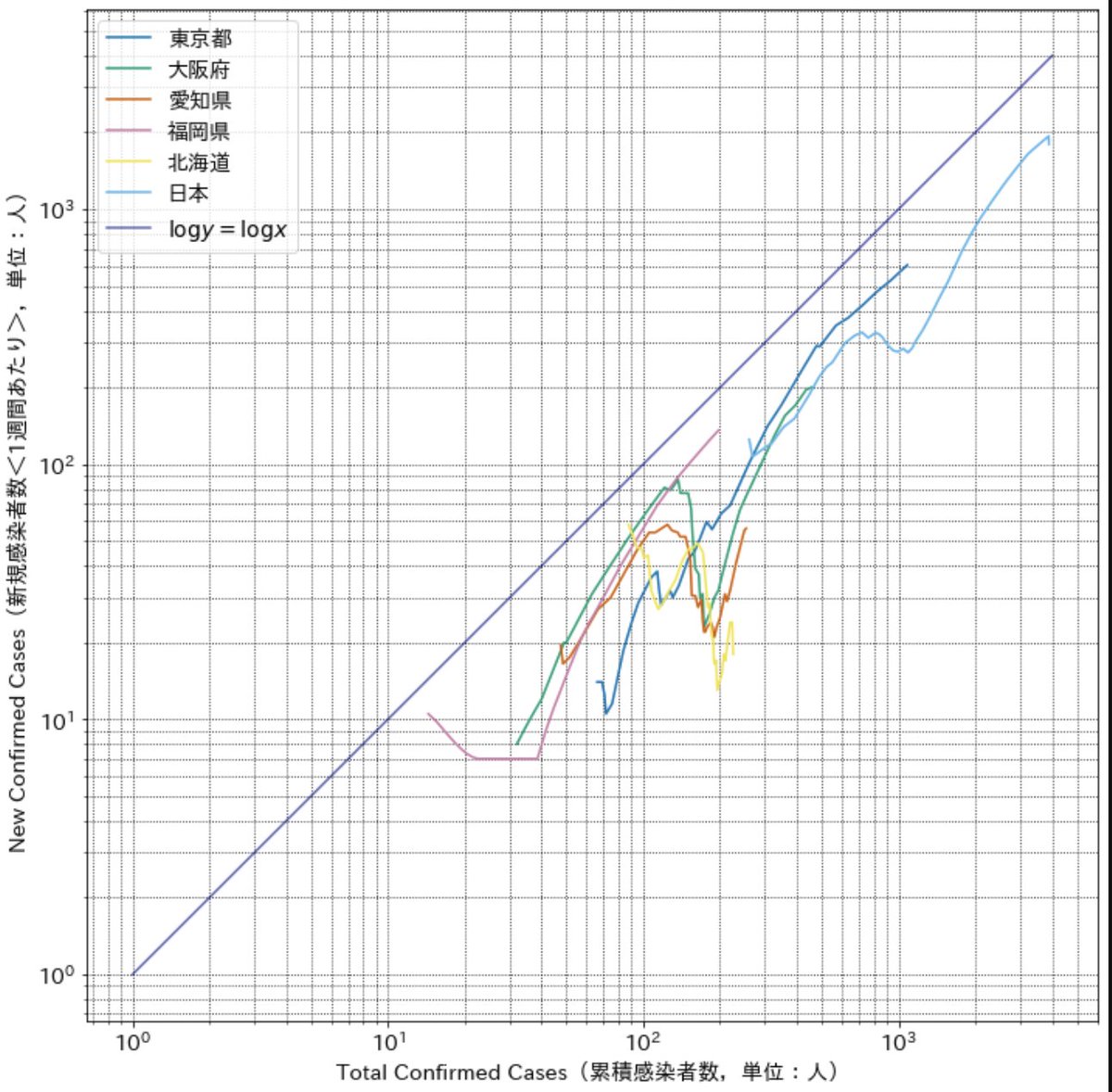



Yusuke Hayashi 林祐輔 X 累積感染者数 と Dx Dt 新規感染者数 の両対数グラフ X が指数増加 Dx Dt A X するとき 両対数にすると Log Dx Dt C Log X となって グラフの傾きは A によらず 1 になる 都市別に両対数グラフを描くと 東京は




Jun Rekimoto 暦本純一 両対数グラフ の最新だと中国韓国オーストラリアは指数的成長から離脱 日本は本当に瀬戸際 傾き1の線に載っていると指数関数的成長 T Co 2w8hugve49




第2節 運動の法則



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方




Welcome To Adobe Golive 5



2 3 2 対数 対数 両対数グラフ



電気基礎実験 グラフ処理 Ppt Download



両対数グラフ 雲外蒼天



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方



片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説



対数グラフ



Excel エクセルで両対数グラフを作成する方法 両対数の傾きの意味は



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方



対数グラフ



Zabbix 3 0 の予測機能のための数学的理解




倍になるのはいつか 緒方 壽人 Takram Note
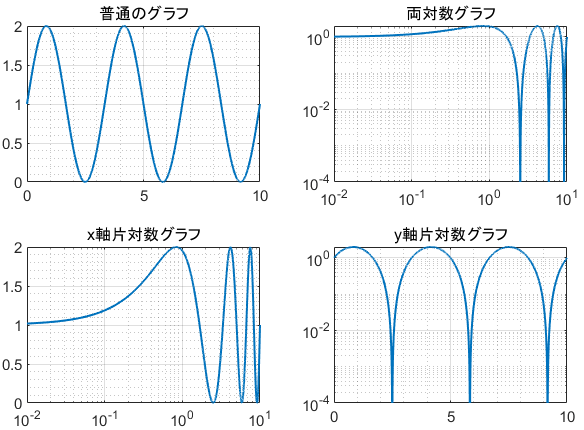



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説



この画像の片対数グラフの直線式の求め方を詳しく教えてください 片対数グ Yahoo 知恵袋
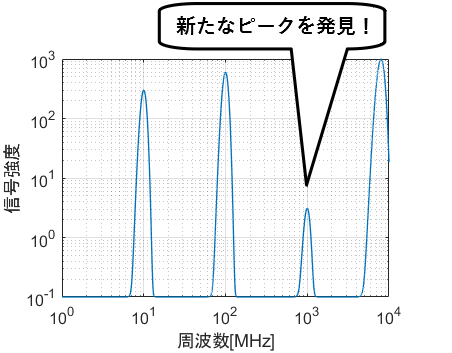



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説




Lazy Life Easy Exit




片対数 両対数グラフ うさぎでもわかる実験の基礎 第3羽 片対数 両対数グラフを用いた最小2乗法 工業大学生ももやまのうさぎ塾



対数グラフを作成する エクセル13基本講座



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方




08 号 光計測装置及び光計測装置の調整方法 Astamuse



講義ニュース 3 2004年度 岡田成幸のhp




両対数グラフ Wikipedia



磁石の磁束密度をテスラメータで測定するという実験を行ったのですが 写真の両対数 Yahoo 知恵袋
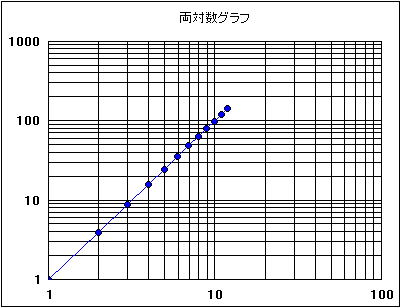



対数グラフ
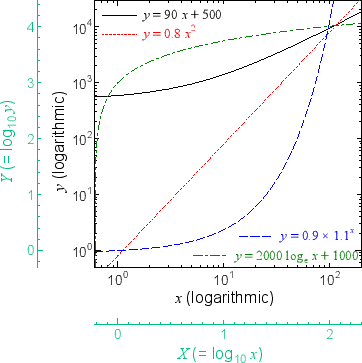



2 1 4 対数 対数 両対数グラフ
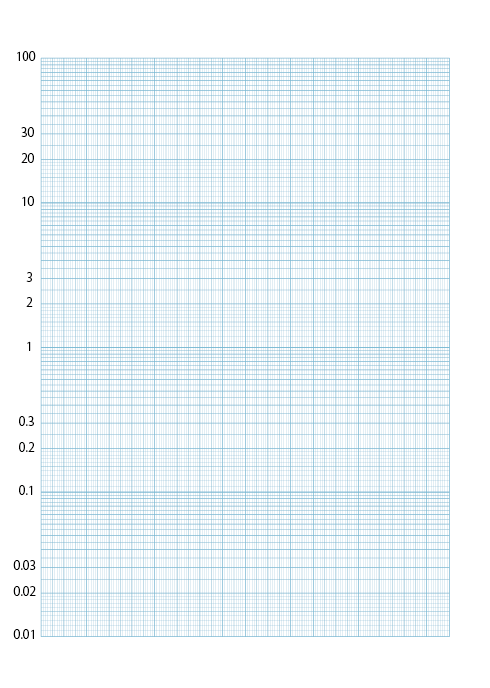



対数グラフとは何か Emanの物理数学




片対数グラフ 両対数グラフの傾きの意味 高校数学の美しい物語
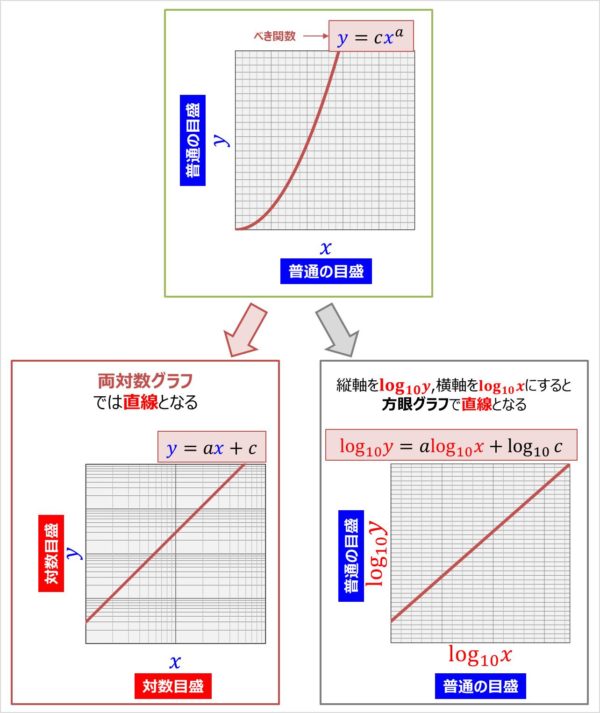



片対数グラフと両対数グラフとは 読み方 や 傾き の意味などを解説
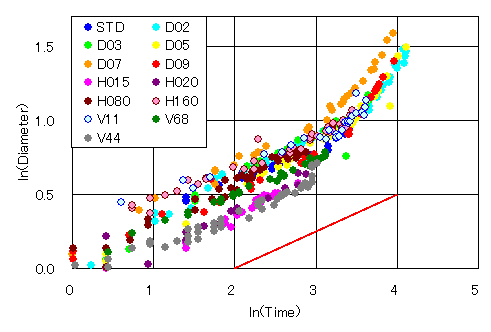



4 3 表面張力波解



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方
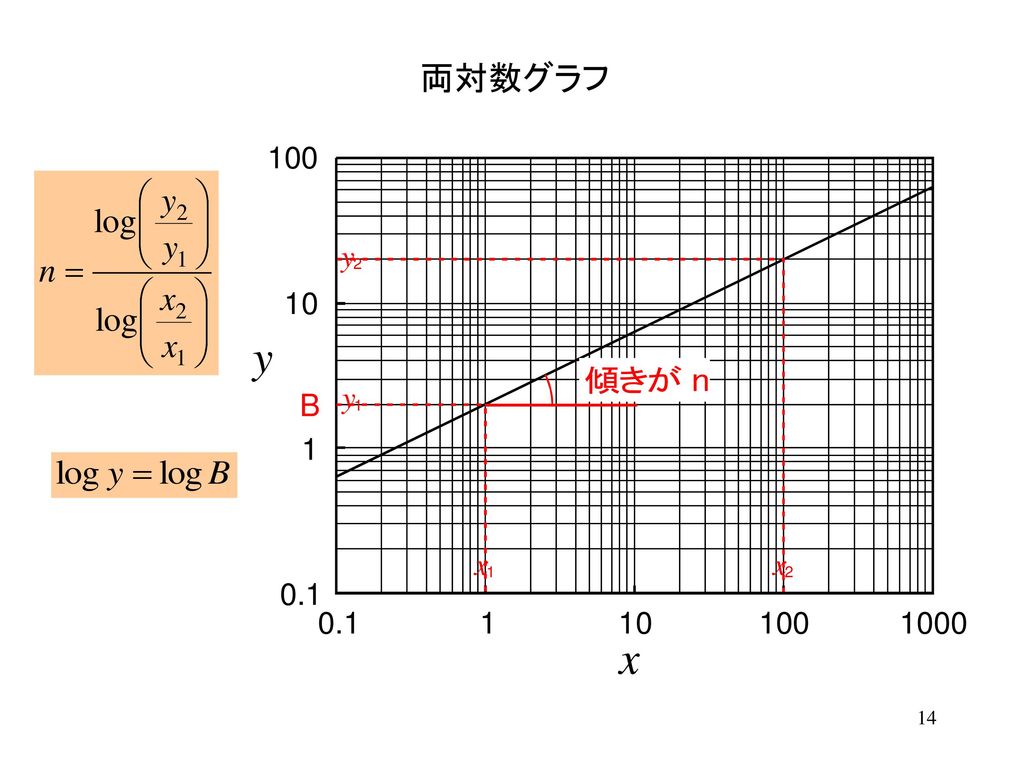



電気基礎実験 グラフ処理 Ppt Download
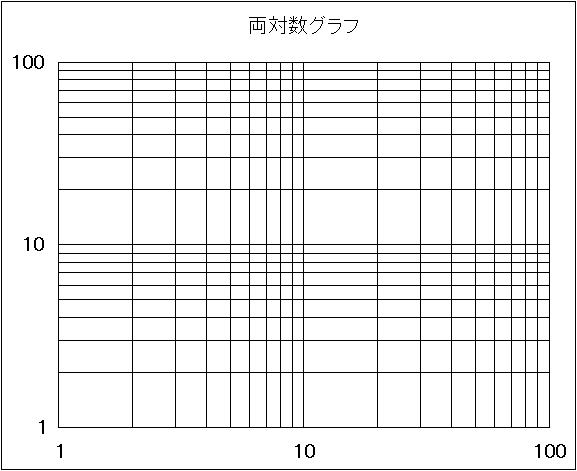



対数グラフ
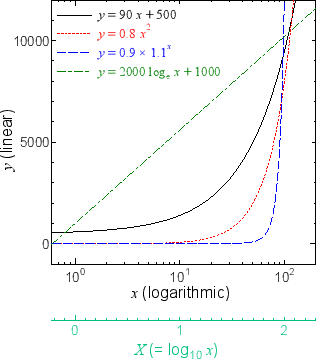



2 1 3 対数 線形 片対数グラフ
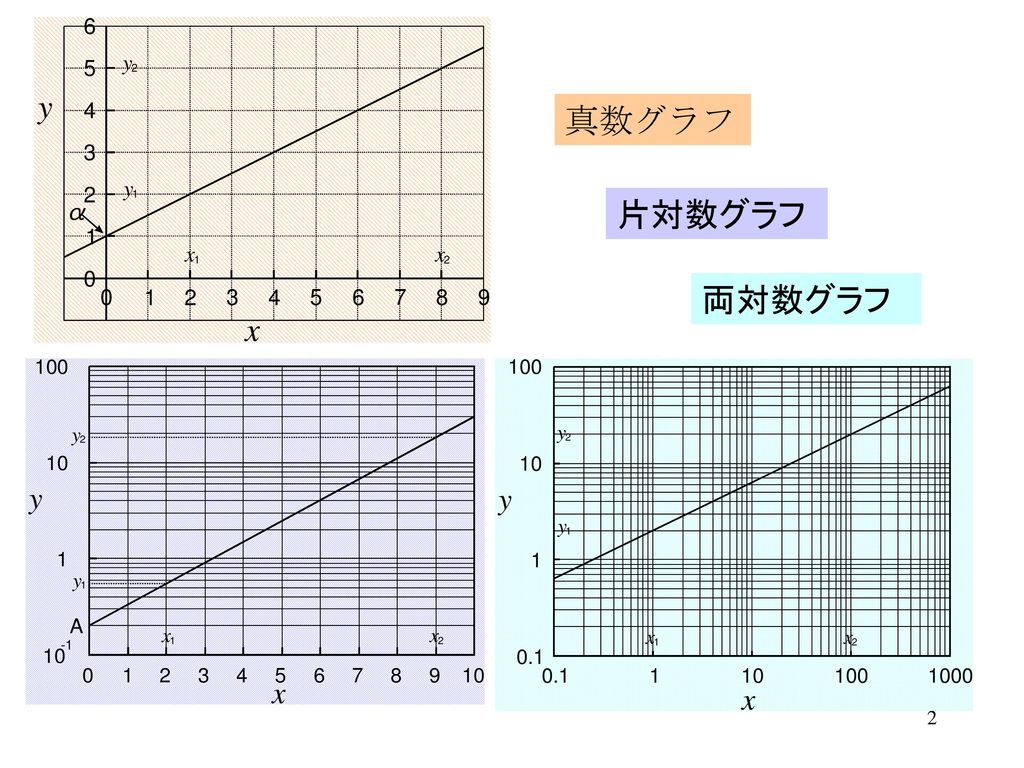



電気基礎実験 グラフ処理 Ppt Download



最小二乗法 指数近似と累乗近似 最小二乗法のうち 指数近似と累乗近似をする場合について考えてみましょう 世の中の現象は 決して線形的な関係ばかりではありません むしろ 指数関数的な変化や 累乗関数的な変化になることが多いものです
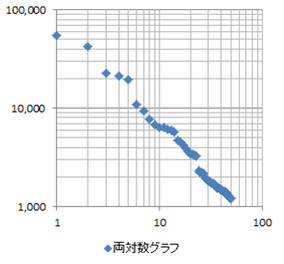



対数グラフの作り方 創発企画



3 対数グラフの利便性




Welcome To Adobe Golive 5
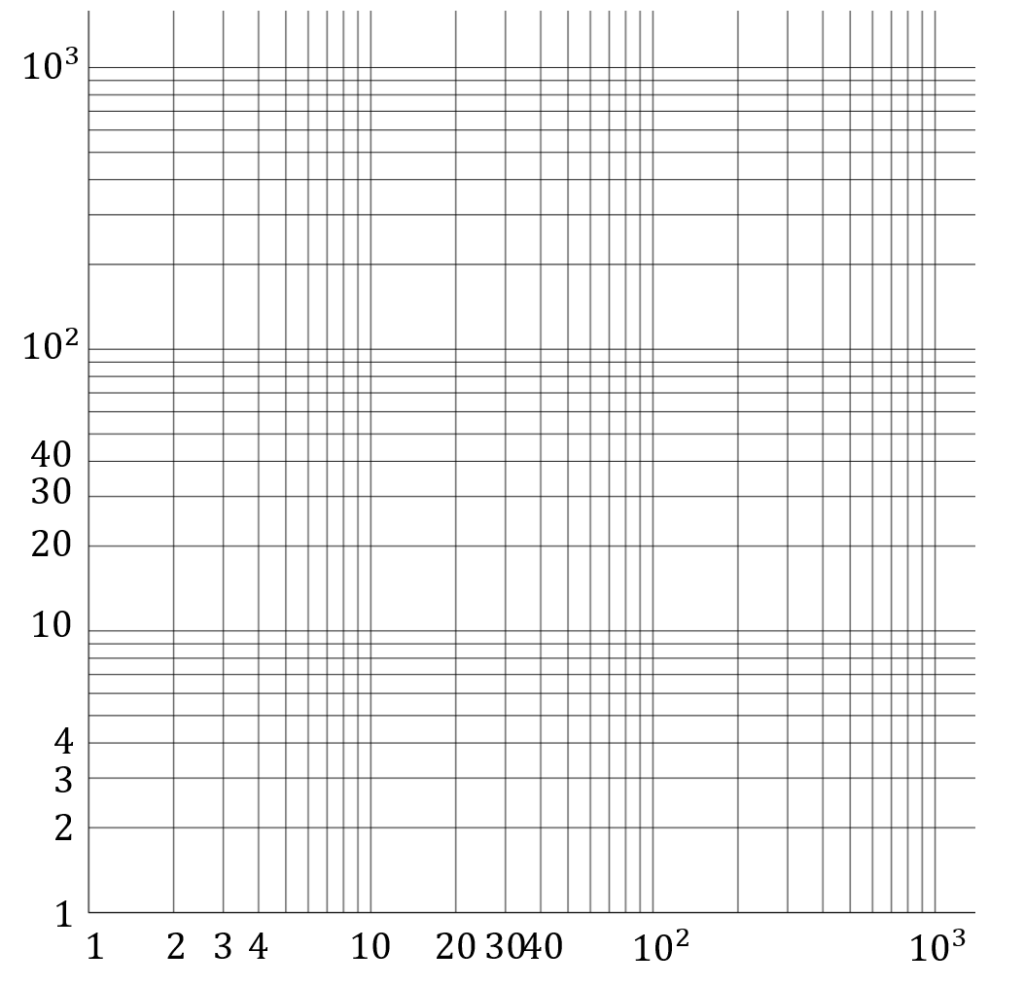



対数グラフ 片対数グラフ 両対数グラフとその意味 数学の景色



片対数グラフの傾きの求め方なのですが 1 10 5 2 Yahoo 知恵袋



実習補足説明



3
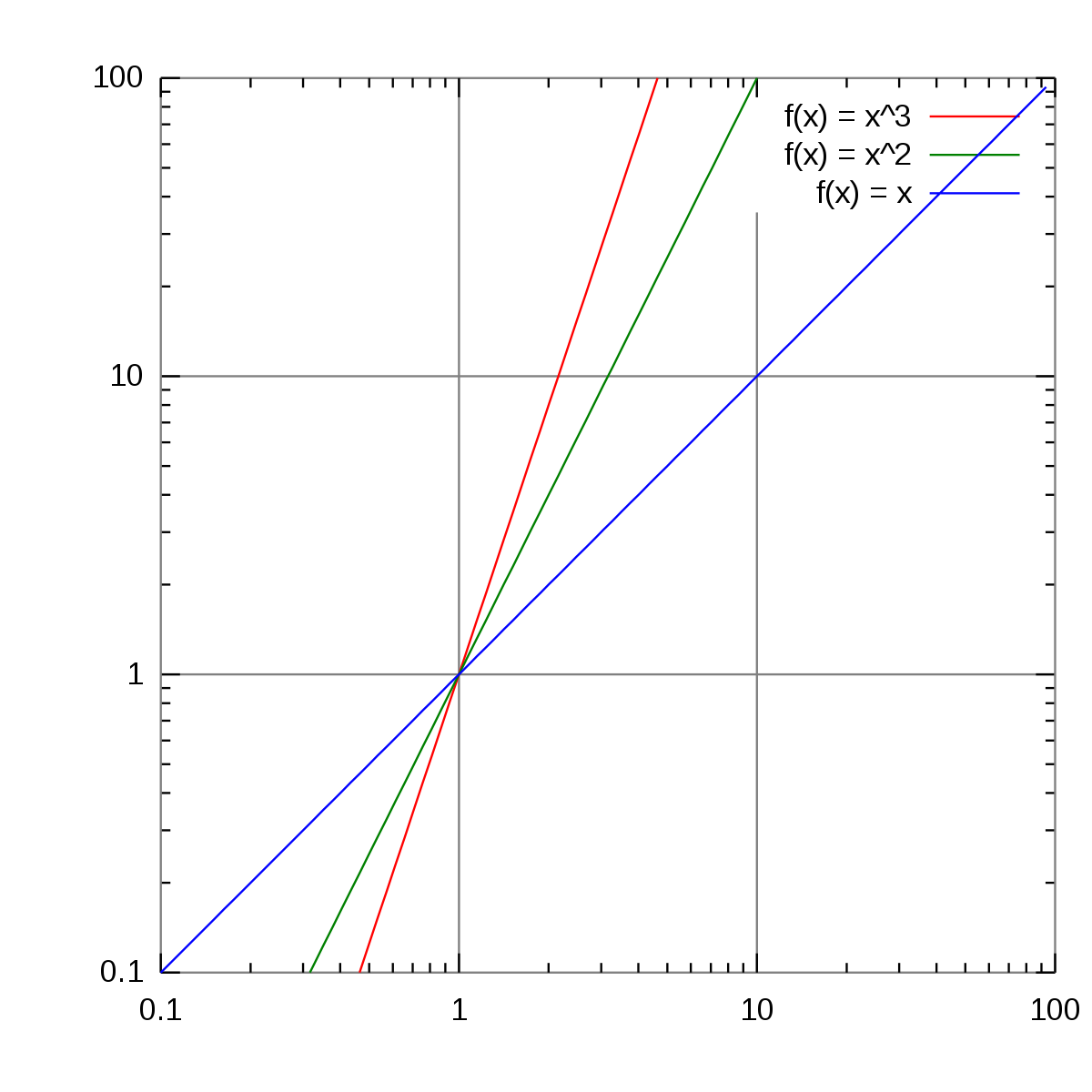



両対数グラフ Wikipedia
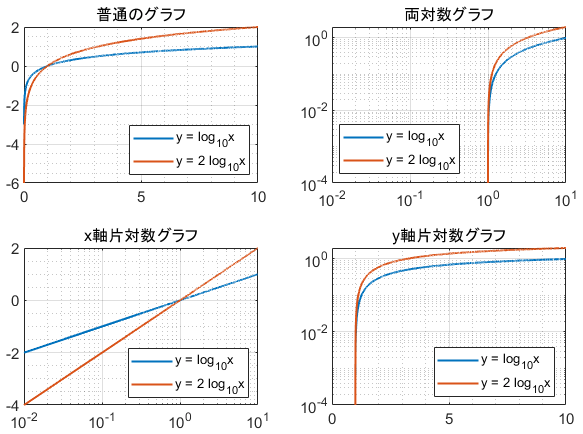



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説
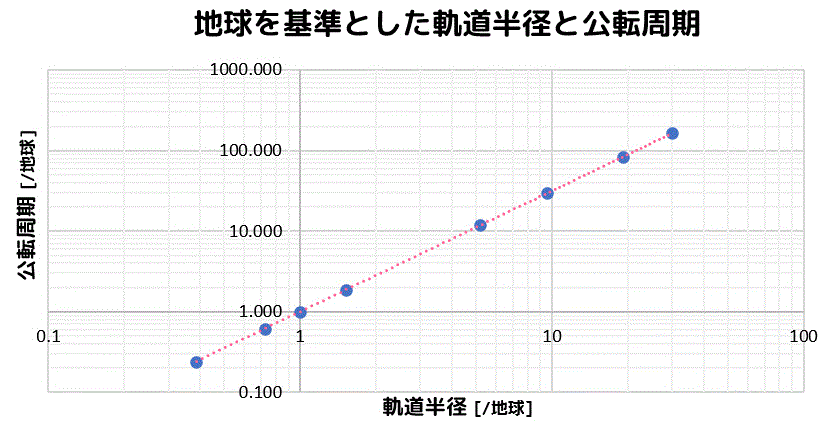



片対数 両対数グラフ うさぎでもわかる実験の基礎 第3羽 片対数 両対数グラフを用いた最小2乗法 工業大学生ももやまのうさぎ塾




Jun Rekimoto 暦本純一 両対数グラフ の最新だと中国韓国オーストラリアは指数的成長から離脱 日本は本当に瀬戸際 傾き1の線に載っていると指数関数的成長 T Co 2w8hugve49




対数目盛を含むグラフ上での最小二乗法の実装 Codezine コードジン



1




Welcome To Adobe Golive 5



半導体 電子デバイス物理 実験 一般的注意事項 レポートの書き方




両対数グラフ Emanの物理数学
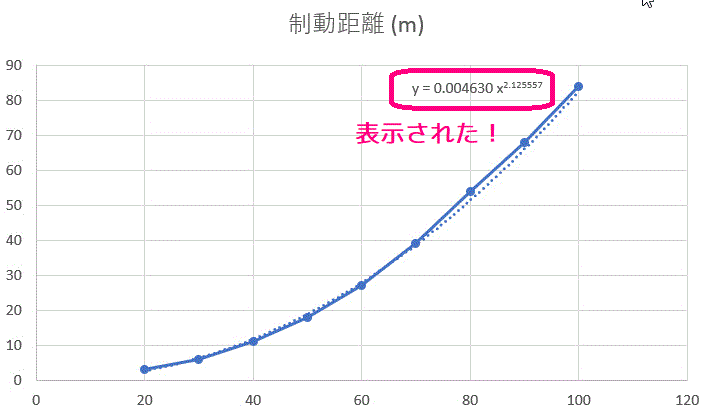



片対数 両対数グラフ うさぎでもわかる実験の基礎 第3羽 片対数 両対数グラフを用いた最小2乗法 工業大学生ももやまのうさぎ塾
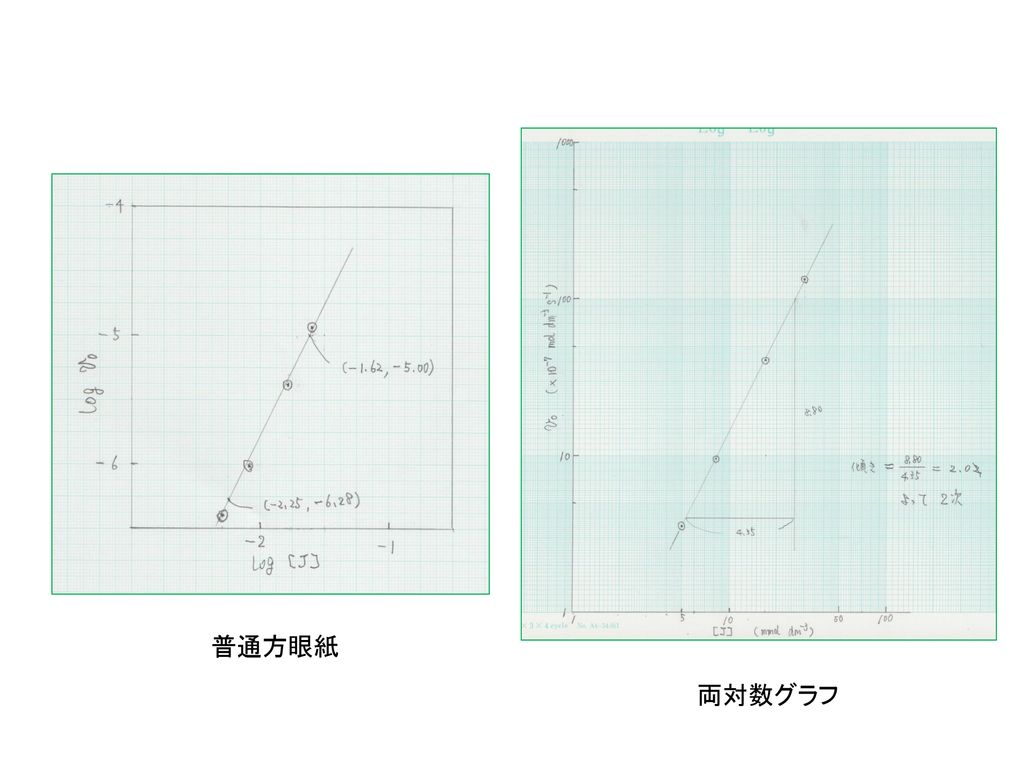



課題 1 普通方眼紙および両対数グラフ用紙の両方で表示せよ Ppt Download
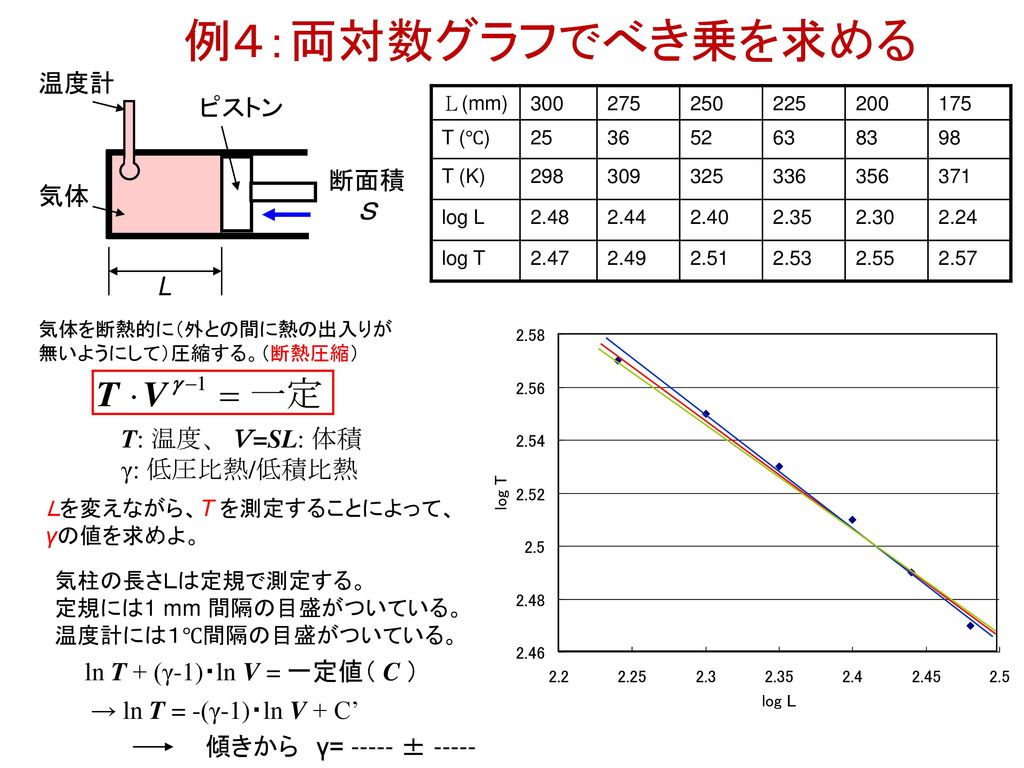



国際物理オリンピック実験試験のシラバス 1 標準的な実験器具 装置が使える マニュアル無しで使える Ppt Download
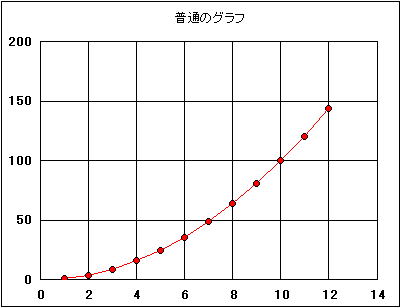



対数グラフ



実験結果の整理



エクセル10の両対数グラフの傾きについての質問です Yahoo 知恵袋



対数グラフ




対数グラフを計算式に直す方法 学校で習ったと思うのですがすっかり忘 数学 教えて Goo
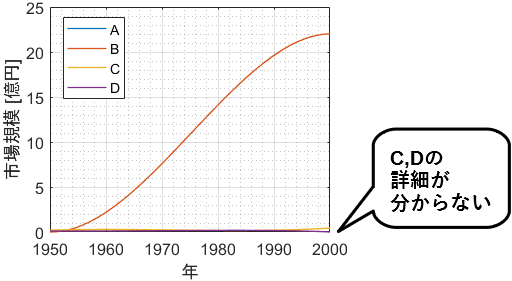



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説



片対数グラフ 両対数グラフとは 読み方 書き方 使い方を解説



1
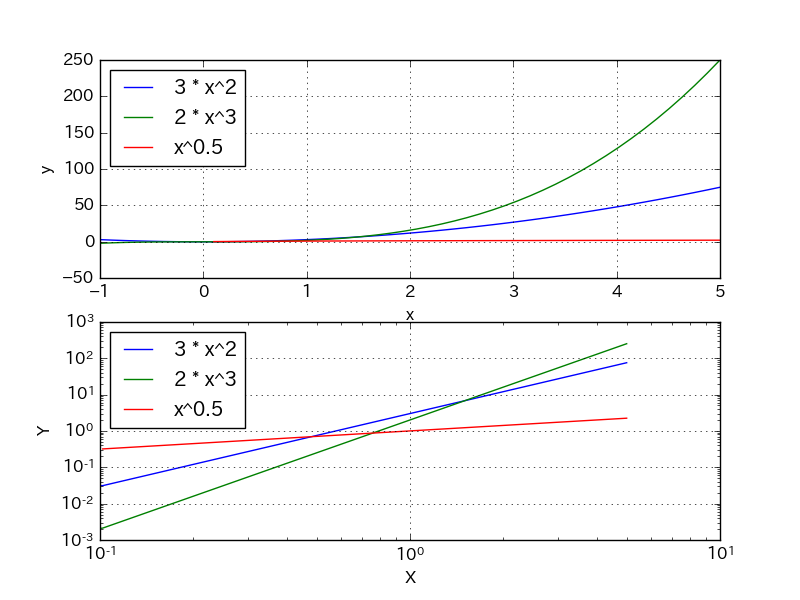



指数と対数 その2 累乗と累乗根 対数グラフ ふシゼン



0 件のコメント:
コメントを投稿